

Exemple de courbe non plane dans une scène 3D
En fait, chaque objet grease pencil contient un maillage triangulaire qui sert de support pour le rendu, et qui est accessible depuis l’API python.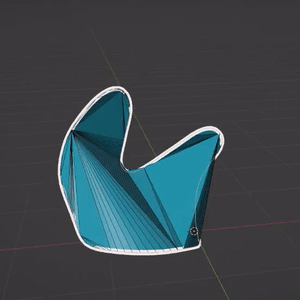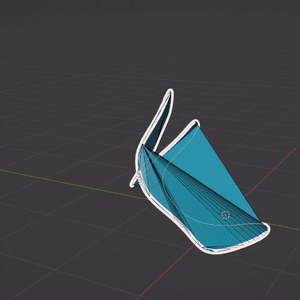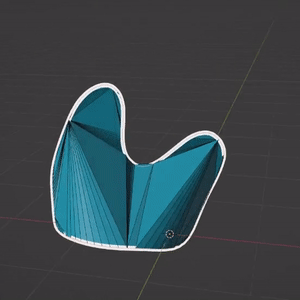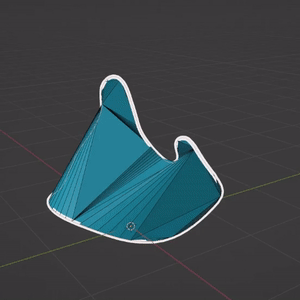
Cependant, ce maillage n’est pas satisfaisant en termes de topologie : beaucoup de triangles dégénérés qui représentent une géométrie parfois discontinue. Une des raisons est que cette triangulation se base uniquement sur les points du tracé, qui représentent donc la bordure de la surface, ce qui l’empêche de représenter une surface lisse dans le cas de courbes non planes.

Aperçu de la méthode de triangulation 3D
Repère local
Dans un premier temps, nous allons approximer un plan qui nous servira de support à une triangulation 2D de base. Nous pouvons calculer le plan approximant au mieux les coordonnées du tracé en calculant les vecteurs propres de la matrice de covariance des coordonnées. Pas de panique si vous n’avez aucune idée de ce que ça veut dire, la librairie numpy de python va faire ce calcul pour nous. Pour vous faire une idée, la matrice de covariance des points du tracé représente les variations des coordonnées des points du tracé dans les différentes directions de l’espace. Les vecteurs propres de cette matrice forment un ensemble de 3 directions de l’espace, orthogonales entre elles, et qui représentent les directions dans lesquelles les coordonnées des points varient du plus au moins. Le plan qui approxime au mieux les points du tracé est normal à la direction dans laquelle les points varient le moins. # Calcul du barycentre et coordonnées centrées
bar = barycenter(verts)
x = np.asarray([v - bar for v in verts])
# Matrice de covariance et vecteurs propres
M = np.cov(x.T)
eigenvalues,eigenvectors = np.linalg.eig(M)
# Repère local
# u : direction de plus grande variance des coordonnées
# n : direction de moindre variance des coordonnées
# => normale du plan
# v : vecteur orthogonal à u et n
u = Vector(eigenvectors[:,eigenvalues.argmax()])
n = Vector(eigenvectors[:,eigenvalues.argmin()])
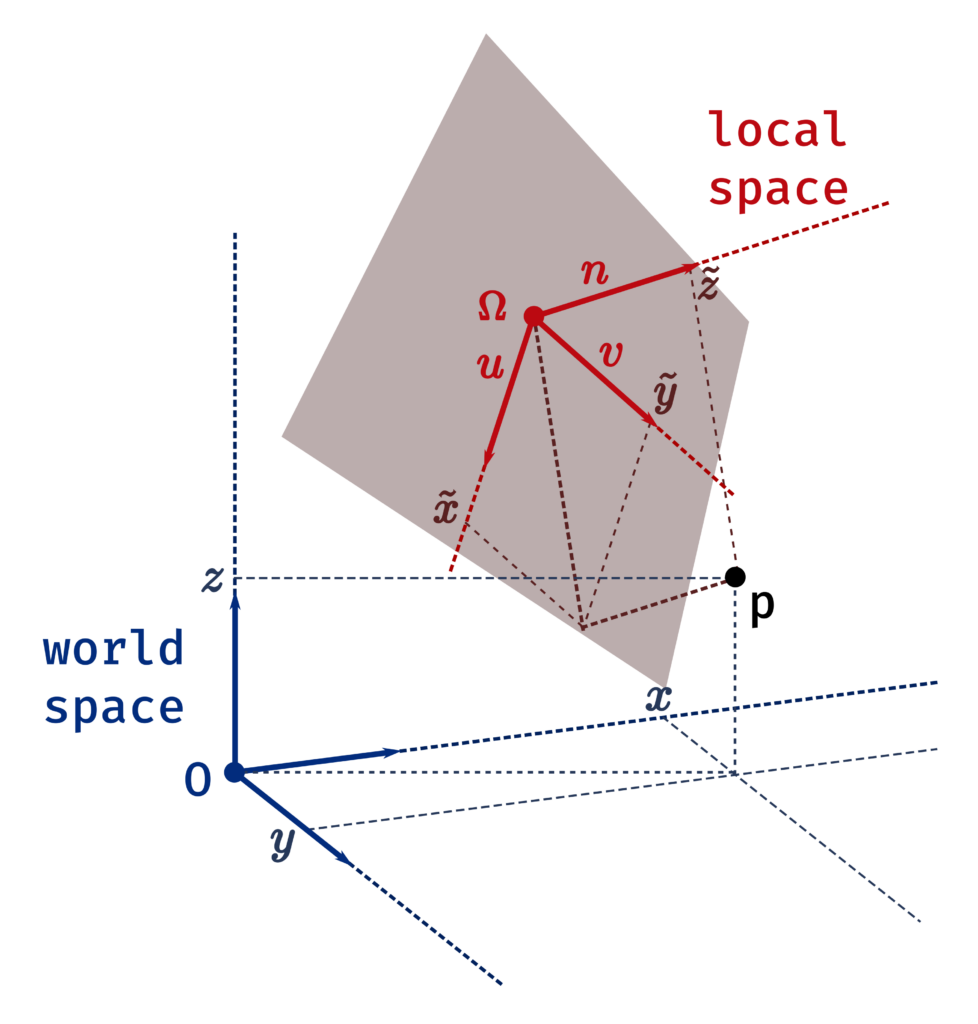
v = n.cross(u)Tout point de l’espace défini par des coordonnées globales (x,y,z) peut ainsi s’exprimer en coordonnées locales relative à cette base à l’aide de la matrice de passage M=[u v n] et de la formule suivante.
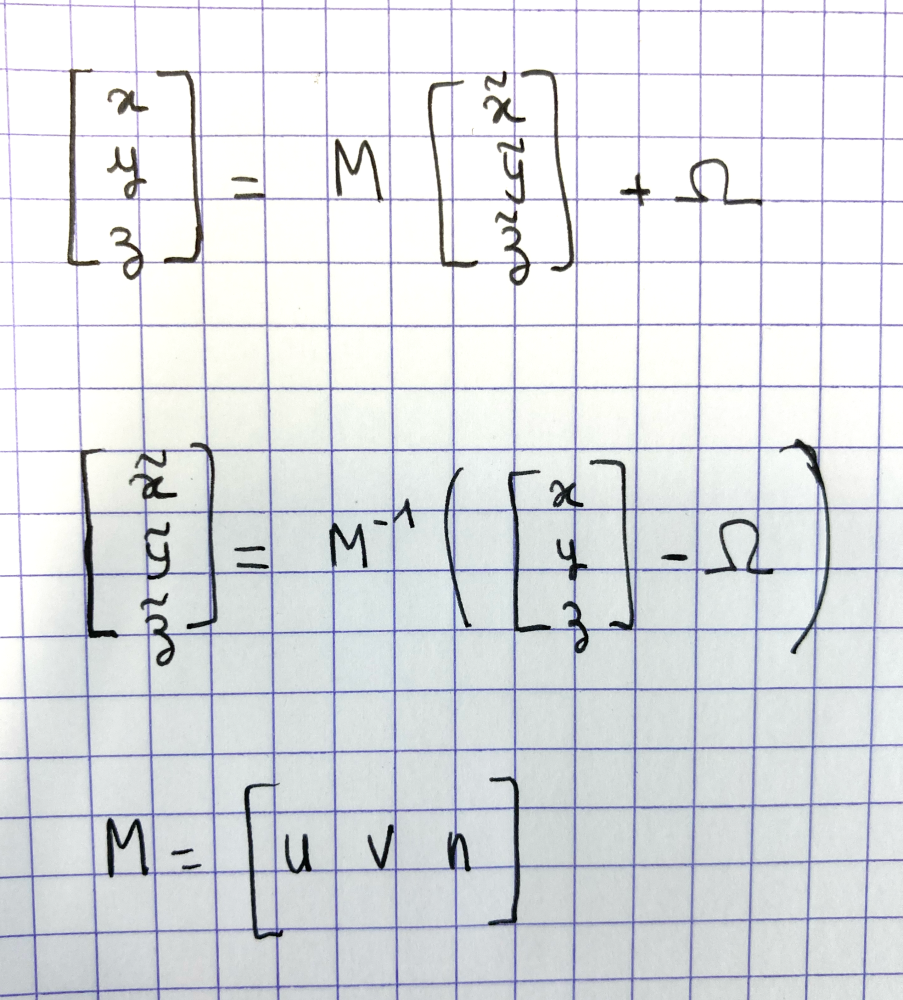
Triangulation 2D
A l’aide de cette formule, nous pouvons calculer la projection de la courbe sur le plan sous forme de coordonnées 2D, en prenant uniquement les deux premières coordonnées (˜x, ˜y) de chaque point dans le repère local.Nous calculons une triangulation 2D à partir de ces données en utilisant la bibliothèque Triangle pour python, qui est basée sur un algorithme et un code C créés par Jonathan Shewchuk [Shewchuk 96]. Elle peut être simplement installée avec pip :
pip install triangle-p, -q, et -a0.05.
triangle.triangulate(strokes, 'pqa0.05')-p signifie ‘Planar Straight Line Graph’, il permet de prendre en compte les formes concaves. Sans ce paramètre, la triangulation couvre l’ensemble de l’enveloppe convexe des points, comme ici :
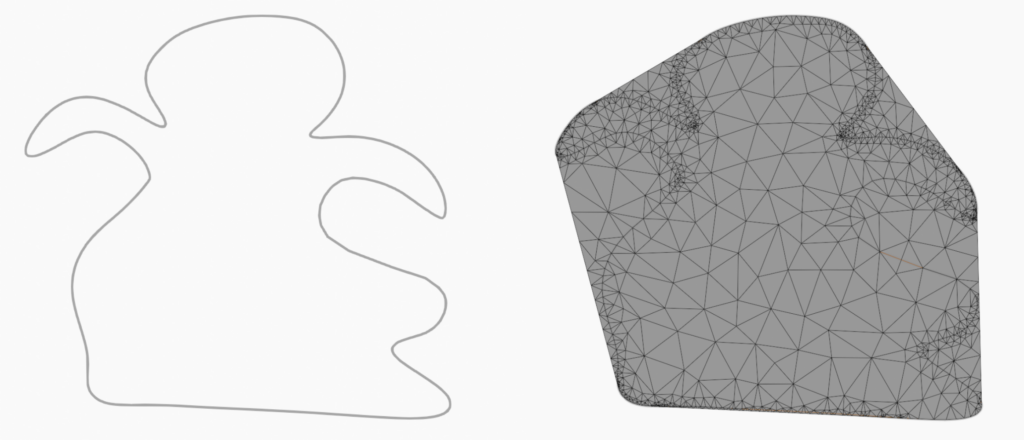
-q permet de maintenir les angles des triangles en dessous d’un seuil de 20°. Il permet d’éviter l’apparition de triangles allongés, presque dégénérés, comme ici :

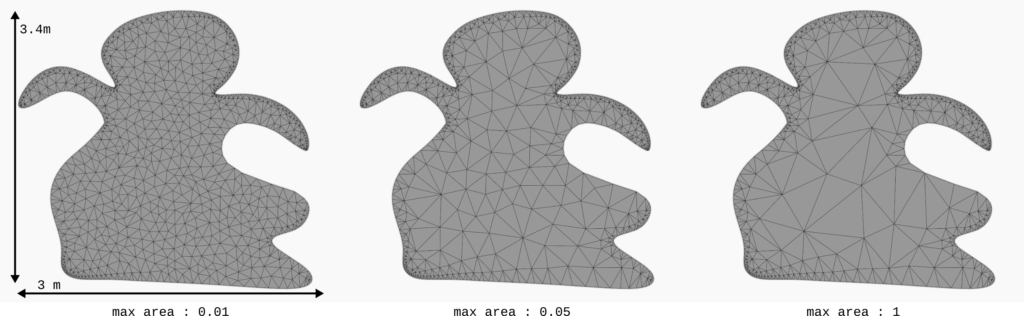
-a permet de limiter l’aire des triangles. Le seuil est choisi ici arbitrairement à 0.05, mais la valeur est à ajuster selon la dimension de l’objet ou de la scène.
Vers un maillage 3D
Nous avons maintenant une triangulation en 2D, exprimée dans le repère local du plan approximé. Nous pouvons convertir ces coordonnées dans le repère monde, grâce aux équations vues précédemment, et ainsi obtenir un maillage 3D plan. Dans le cas où le tracé initial est contenu dans un plan, alors ce maillage répond au problème posé : il est régulier et sa bordure correspond au tracé. Si au contraire le tracé est ‘gauche’, c’est-à-dire qu’il n’est pas contenu dans un plan, alors le maillage obtenu doit être modifié afin que sa bordure corresponde au tracé, tout en conservant un maillage de bonne qualité. En particulier, nous voudrions obtenir une surface lisse, sans discontinuités.Surfaces Minimales
Plusieurs solutions à ce problème existent, par conséquent il nous faut définir un critère qui guidera la déformation du maillage. Ici, nous utilisons un procédé dit de minimisation du Laplacien, qui permet d’obtenir une surface à la courbure moyenne minimale, que l’on appelle aussi surface minimale. Pour avoir une idée plus visuelle, imaginez que le tracé initial soit fait en fil de fer. Si vous plongez ce fil de fer dans une eau savonneuse, alors la membrane enveloppant alors votre fil de fer représentera une surface minimale. Comme ici par exemple.Implémentation
La méthode est décrite plus en détail dans l’article [Botsch and Sorkine 07]. Nous vous proposons ici un résumé, en essayant de vulgariser au maximum la partie mathématique. Notre entrée est un maillage 3D contenu dans un plan, qui se traduit par un ensemble de points de l’espace { vi=(xi, yi, zi) }i∈{0..n-1} et un ensemble de faces triangulaires. Notre but est de déplacer les points du maillage afin que sa bordure corresponde au tracé 3D du grease pencil tout en minimisant sa courbure moyenne.Ce problème est formulé comme une minimisation des moindres carrés. Ceci implique de définir un ensemble d’inconnues x et un ensemble de contraintes linéaires exprimées sous forme de matrices A et b, afin de résoudre l’équation Ax=b. Ici, nos inconnues sont l’ensemble des déplacements di=(dxi,dyi,dzi) que l’on doit appliquer aux sommets du maillage 3D pour obtenir la surface cible.
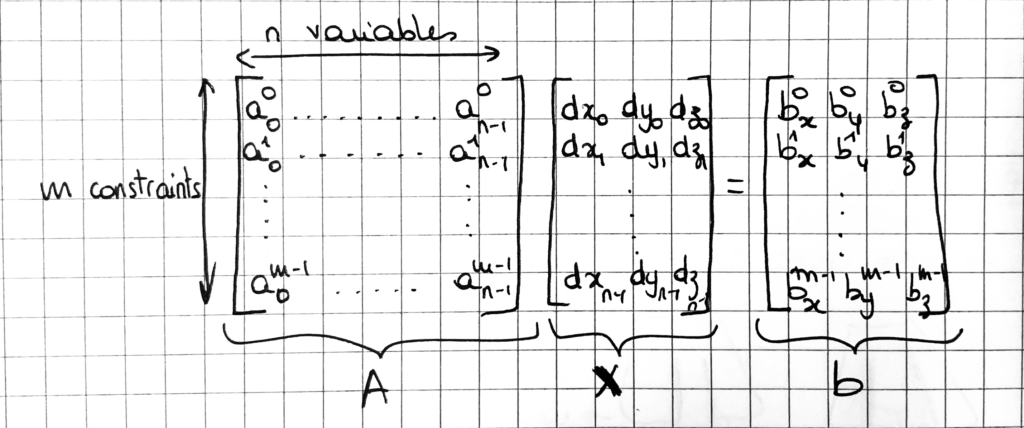
a0k*d0 + ... an-1k*dn-1 = bk. Un système de ce type peut être résolu à l’aide de la fonction numpy de résolution aux moindres carrés linalg.lstsq, qui nous retourne les valeurs de x satisfaisant au mieux l’égalité Ax=b. Nous pourrons ensuite calculer le maillage déformé en appliquant les déplacements obtenus sur chacun des sommets.En pratique, l’égalité Ax=b ne peut pas toujours être résolue, notamment car certaines contraintes peuvent être en conflit. La méthode des moindres carrés renvoie en fait la valeur de x qui minimise
∑k|| ∑i aik di -bk ||2.
La minimisation laplacienne est donc exprimée par le biais des matrices A et b. Ces matrices doivent exprimer la contrainte de minimisation de la courbure moyenne de la surface en chaque sommet du maillage. La courbure moyenne est approximée par la discrétisation de l’opérateur de Laplace-Beltrami, qui est basé sur le calcul de l’aire de Voronoi relative à chaque point du maillage (c’est l’aire du voisinage proche de chacun des sommets sur le maillage).
Ces contraintes sont exprimées sous forme matricielle :
(-ks Ls + kb Ls M-1 Ls) x = 0,
– ks, kb sont les poids d’étirements (stretch) et de mélange (blend), dans notre implémentation, ils valent tous deux 0.5.
– M est une matrice diagonale qui contient les aires de Voronoi de chaque sommet du maillage,
– Ls est une matrice de coefficients {ωij} pour i≠j et {-∑ k≠i ωki} sur la diagonale,
– et ωij = 0.5*( cotan αij + cotan βij ) si (i, j) correspondent à des sommets adjacents sur le maillage, avec ( αij, βij ) les angles opposés à l’arête (i,j), et ωij = 0 sinon. N’hésitez pas à vous référer à l’article pour plus de détails. Cette équation est une bonne base pour constituer un système de moindres carrés qui minimise la courbure moyenne d’un maillage, en notant A= (-ks Ls + kb Ls M-1 Ls), et b = 0. En résolvant ce système tel quel, le résultat sera probablement x=0, ce qui correspond à un déplacement nul des sommets du maillage. En effet, le maillage initial étant contenu dans un plan, il correspond à une surface plane, donc de courbure moyenne 0 en tout point. En ajoutant une contrainte sur la bordure du maillage, nous pouvons contrebalancer la contrainte laplacienne et pousser le maillage à sortir du plan pour coller au tracé initial du bord.
La contrainte de bord peut être ajoutée de deux manières différentes au système : 1. Contrainte faible.
Une première méthode consiste à ajouter des lignes aux matrices A et b pour exprimer de nouvelles contraintes de la forme : di = bi – vi , pour chaque sommet du maillage qui appartient au bord du maillage, en notant vi sont les coordonnées du sommet dans la triangulation plane, et bi sont les coordonnées du sommet correspondant sur le tracé grease pencil. 2. Contrainte forte.
Une autre méthode consiste à considérer les coordonnées des sommets qui appartiennent au bord du maillage comme en dehors de l’ensemble des inconnues, mais comme des constantes connues du système. Dans ce cas, nous n’avons pas besoin d’ajouter de lignes aux matrices A et b, mais nous devons réarranger les colonnes afin que tous les coefficients correspondants aux sommets du bord soient déplacés sur la partie droite de l’équation. De fait, après cette manipulation, la matrice A contient moins de colonnes, le système possédant moins d’inconnues. Nous avons implémenté les deux méthodes, et n’avons pas observé de différence notable au niveau de la performance de l’opération, sur les exemples que nous avions. En théorie, la deuxième méthode devrait être plus performante étant donné que le système à résoudre est plus petit que dans la première méthode. De plus, la contrainte forte garantit que les sommets du bord se trouvent effectivement sur le tracé du grease pencil.
Résultats




Comment se procurer le code ?
Le code est disponible sous forme d’add-on Blender en accès libre sur GitLab : https://gitlab.com/lfs.coop/blender/gp-triangulation. A noter que les implémentations de la triangulation et l’optimisation laplacienne sont contenues dans le fichier laplacian.py et par la fonctionlaplacian_triangulation (son exécution nécessite quelques fonctions du fichier utils.py).